CSE Helper
Powered By Dream Dragon Creation
Binary Tree
Introduction
A binary tree is made of nodes, where each node contains a "left" pointer, a "right" pointer, and a data element. The "root" pointer points to the topmost node in the tree. The left and right pointers recursively point to smaller "subtrees" on either side. A null pointer represents a binary tree with no elements -- the empty tree. The formal recursive definition is: a binary tree is either empty (represented by a null pointer), or is made of a single node, where the left and right pointers (recursive definition ahead) each point to a binary tree.
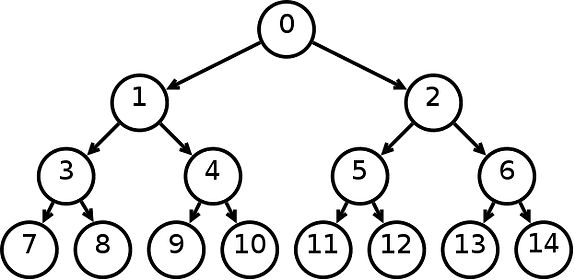
Tree Traversal
If the binary tree is empty
do nothing
Else
N: Visit the root, process data
L: Traverse the left sub-tree
R: Traverse the right sub-tree
(This is Recursive)
Three Traversal Possibilities
In-order traversal
Left sub-tree, Node, Right sub-tree
Pre-order traversal
Node, Left sub-tree, Right sub-tree
Post-order traversal
Left sub-tree, Right sub-tree, Node
Binary Tree - C Program source code
-
#include < stdio.h>
-
#include<stdlib.h>
-
-
struct Node {
-
int value; //store the value of Node
-
int index; // pointer to storing index of the tree
-
struct Node* leftChild; // pointer to the left Node
-
struct Node* rightChild; // pointer to the right Child
-
};
-
-
struct Node* root; // global variable - pointer for root of the tree
-
int numElements; // global variable - no of elements in the tree
-
-
int add_left_child(Node* parent, int inputValue){
-
Node* newLeaf;
-
if (parent->leftChild == NULL){
-
newLeaf = new Node( );
-
parent->leftChild = newLeaf;
-
newLeaf->value = inputValue;
-
return 1;
-
}
-
else{
-
return -1;
-
}
-
}
-
-
int add_right_child ( Node* parent , int inputValue ){
-
Node* newLeaf;
-
if ( parent->rightChild == NULL ){
-
newLeaf = new Node( );
-
parent->rightChild = newLeaf;
-
newLeaf->value = inputValue;
-
return 1;
-
}
-
else{
-
return -1;
-
}
-
}
-
-
struct Node* create_Tree( int inputArray[ ] , int index , int arraySize ) {
-
numElements = arraySize; // store the number of elements in the array
-
root = new Node ( ) ;
-
root->value = inputArray [ index ] ;
-
root->index = index;
-
//if left child node excised the index of array return null, thats leaf
-
if ( ( 2 * index + 1 ) >= arraySize ) {
-
return root;
-
}
-
//adding left child node
-
if ( add_left_child ( root , inputArray[2 * index + 1] ) ) {
-
root->leftChild = create_Tree( inputArray , ( 2 * index + 1 ) , arraySize ) ;
-
}
-
//if right child node excised the inex of array return null, thats leaf
-
if ((2 * index + 2 ) >= arraySize ){
-
return root;
-
}
-
// adding right child node
-
if (add_right_child(root, inputArray [2 * index + 2 ] ) ) {
-
root->rightChild = create_Tree ( inputArray , ( 2 * index + 2 ) , arraySize ) ;
-
}
-
return root; // return the sub tree node pointer
-
}
-
-
// pre- order traversal : *Node *Left sub Tree *Right sub Tree
-
void traverse_preorder(Node* root){
-
if ( root )
-
{ printf ( root->value + " " ) ;
-
traverse_preorder ( root->leftChild ) ;
-
traverse_preorder ( root->rightChild ) ;
-
}
-
}
-
-
//post order Traversal : *Left sub Tree * Right sub Tree * Node
-
void traverse_postorder ( Node* root ) {
-
if ( root )
-
{ traverse_postorder( root->leftChild ) ;
-
traverse_postorder( root->rightChild ) ;
-
printf ( root->value + " " ) ;
-
}
-
}
-
// In-order Travesal : *Left sub Tree *Node *Right sub Tree
-
void traverse_inorder( Node* root ){
-
if ( root ){
-
traverse_inorder ( root->leftChild ) ;
-
printf ( root->value + " " ) ;
-
traverse_inorder ( root-> rightChild ) ;
-
}
-
}
-
// to expand methord
-
void get_inputOrder ( Node* root , int inputs[ ] ) {
-
if ( root )
-
{ inputs [ root->index ] = root->value;
-
get_inputOrder ( root->leftChild , inputs ) ;
-
get_inputOrder( root->rightChild , inputs ) ;
-
}
-
}
-
-
Node* expand_Tree(Node* root , int elements[ ] , int ArraySize ){
-
int allElements = numElements + ArraySize;
-
int NewArray[12]; // int allElement should be the array size but in V S it consider as not constant value therefore i had to set it manually
-
get_inputOrder(root, NewArray); // get all the elements in the Tree and put in to array
-
int j = 0;
-
for (int i = 8; i < allElements; i++){
-
NewArray [ i ] = elements [ j ];
-
j++;
-
}
-
return create_Tree(NewArray, 0, allElements); // all elemtment put in to the one new aray and create new tree and return the root
-
}
-
-
int main( ) {
-
printf( "Create tree [1,45,23,33,25,53,54,11] \n");
-
int array [ 8 ] = { 1, 45, 23, 33, 25, 53, 54, 11 };
-
Node* Root = create_Tree(array, 0, 8);
-
printf ( " InOrderTraversal of Tree : \n ");
-
traverse_inorder ( Root ) ;
-
printf( " \n " ) ;
-
printf(" pre- order traversal : \n " );
-
traverse_preorder(Root);
-
printf( "\n");
-
printf("post order Traversal :\n");
-
traverse_postorder(Root);
-
printf("\n");
-
printf("\n \n" );
-
printf("Expand the same tree [3,22,7,64] \n ");
-
int expand[] = { 3, 22, 7, 64 };
-
Root = expand_Tree(Root, expand, 4);
-
printf( "InOrderTraversal of Tree :\n ");
-
traverse_inorder(Root);
-
printf( "\n" );
-
printf("pre- order traversal : \n" );
-
traverse_preorder(Root);
-
printf("\n" );
-
printf( "post order Traversal :\n" );
-
traverse_postorder(Root);
-
printf( "\n" );
-
}