Heap Sort

Introduction

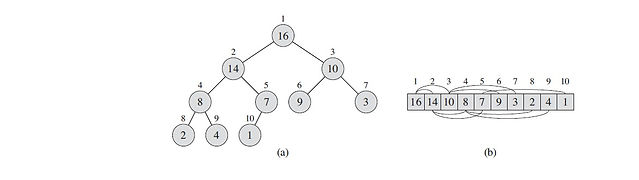
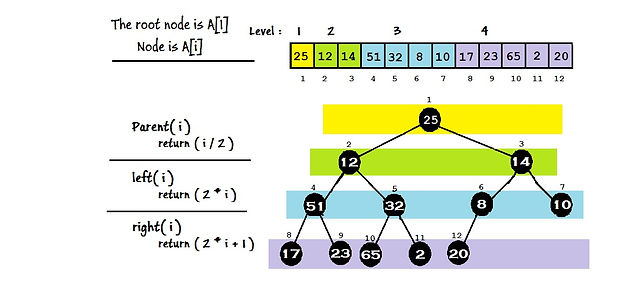
The binary heap data structures is an array that can be viewed as a complete binary tree. Each node of the binary tree corresponds to an element of the array. The array is completely filled on all levels except possibly lowest.

By the definition of a heap, all the tree levels are completely filled except possibly for the lowest level, which is filled from the left up to a point. Clearly a heap of height h has the minimum number of elements when it has just one node at the lowest level. The levels above the lowest level form a complete binary tree of height h -1 and 2^h -1 nodes. Hence the minimum number of nodes possible in a heap of height h is 2^h. Clearly a heap of height h, has the maximum number of elements when its lowest level is completely filled. In this case the heap is a complete binary tree of height h and hence has 2^(h+1) -1 nodes.

Maintaining the heap property

In order to maintain the max-heap property, we call the procedure MAX-HEAPIFY. Its inputs are an array A and an index i into the array. When it is called, MAXHEAPIFY assumes that the binary trees rooted at LEFT ( i ) and RIGHT( i ) are maxheaps, but that AOEi might be smaller than its children, thus violating the max-heap property. MAX-HEAPIFY lets the value at A [ i ] “float down” in the max-heap so that the subtree rooted at index i obeys the max-heap property.

Max- heapify Example

I'm a paragraph. Click here to add your own text and edit me. I’m a great place for you to tell a story and let your users know a little more about you.

Building a heap

We can use the procedure MAX-HEAPIFY in a bottom-up manner to convert an array

A[ 1 . . . n ], where n = A.length, into a max-heap. The procedure BUILD-MAX-HEAP goes through the remaining nodes of the tree and runs MAX-HEAPIFY on each one

BUILD-MAX-HEAP( A )

1 A.heap-size = A.length

2 for i = [A.length /2 ] downto 1

3 MAX-HEAPIFY (A , i )

HeapSort Algorithm

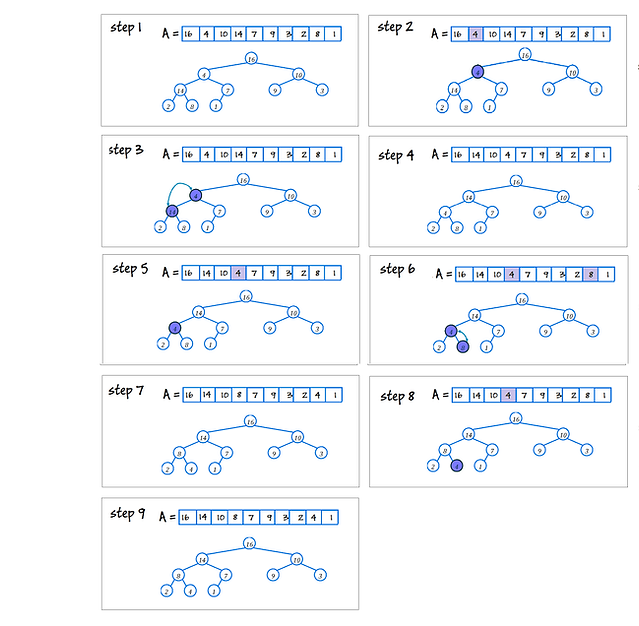
The heapsort algorithm starts by using BUILD-MAX-HEAP to build a max-heap on the input array A [ 1 . . . n], where n = A.length. Since the maximum element of the array is stored at the root A[ 1 ], we can put it into its correct final position by exchanging it with A[ n ]. If we now discard node n from the heap—and we can do so by simply decrementing A.heap-size—we observe that the children of the root remain max-heaps, but the new root element might violate the max-heap property. All we need to do to restore the max-heap property, however, is call MAX-HEAPIFY( A , 1 ), which leaves a max-heap in A [1 . . . n-1]. The heapsort algorithm then repeats this process for the max-heap of size n-1 down to a heap of size 2.

HEAPSORT ( A )

1 BUILD-MAX-HEAP( A )

2 for i = A.length downto 2

3 exchange A [1 ] with A [ i ]

4 A.heap-size = A.heap-size 1

5 MAX-HEAPIFY (A , 1 )

Heap Sort - C++ source Code

Using this sample code you can implement Max-Heapify Data Structure, Heapsort and priority Queue data structure

1 #include <iostream>
2 #include <cstdio>

3 using namespace std;
4 struct Tuple
5 {
6            int Priority;
7            int Value;
8 };

9 int QueueSize;

10
11 //contractor funtion of print parameter with pointer to array
12 void print(Tuple* a) {
13            for (int i = 0; i <QueueSize; i++) {
14                      cout << a[i] Value << " ";
15            }
16            cout << endl << endl;
17 }
18 //This function will return the index of the parent node of the node i
19 int parent(int i) {
20            if (i == 1)
21                      return 0;
22            if (i % 2 == 0)
23                      return ((i / 2) - 1);
24            else
25                      return ((i / 2));
26 }

27 //This function will return the index of the left child node of the node i
28 int left(int i) {
29            return (2 * i) + 1;
30 }

31 //This function will return the index of the right child node of the node i
32 int right(int i) {
33            return (2 * i) + 2;
34 }

35 /*Given a node i, with left child l and a right child r and with both the sub -trees rooted by l and r are max-heaps,
36 this function will convert the sub-tree rooted by node i a max-heap */
37 void heapify(Tuple a[], int i) {
38            int l = left(i), great;
39            int r = right(i);
40            if ((a[l] Priority > a[i] Priority) && (l < QueueSize)) {
41                      great = l;
42            }else {
43                      great = i;
44            }
45            if ((a[r] Priority > a[great] Priority) && (r < QueueSize)) {
46                      great = r;
47            }
48            if (great != i) {
49                      Tuple tempValue = a[i];
50                      a[i] = a[great];
51                      a[great] = tempValue;
52                      heapify(a, great);
53            }
54 }

55 //This function will convert the specified array into a max-heap
56 void BuildMaxHeap(Tuple a[]) {
57            for (int i = 0 / 2; i <= (QueueSize - 1); i++) {
58                      heapify(a, i);
59            }
60 }

61 //transform a specified array to a sorted array
62 void HeapSort(Tuple a[]) {
63            BuildMaxHeap(a);
64            for (int i = QueueSize; i > 0; i--) {
65                      int temp = a[0] Value;
66                      a[0] = a[QueueSize - 1];
67                      a[QueueSize - 1] Value = temp;
68                      QueueSize = QueueSize - 1;
69                      heapify(a, QueueSize);
70            }
71 }

72 //This function will return the maximum element in the heap
73 int HeapMaximum(Tuple a[]){
74            HeapSort(a);
75            return a[QueueSize - 1] Value;
76 }

77 //This function will remove the maximum element from the heap and return it
78 Tuple* HeapExtractMax(Tuple a[]){
79            HeapSort(a);
80            Tuple newArr[7];
81            for (int i = 0; i < (QueueSize - 1); i++){
82                      newArr[i] = a[i];
83            }
84            QueueSize--; // decrement the array size by 1
85            a = newArr;
86            return a;
87 }

88 //This function will insert the specified element to the max heap
89 void MaXHeapInsert(Tuple a[], int newValue){
90            Tuple newArr[11];
91            for (int i = 0; i < (QueueSize); i++){
92                      newArr[i] = a[i];
93            }
94            newArr[QueueSize] Value = newValue;
95            QueueSize++; // increment the array size by 1
96            BuildMaxHeap(newArr);
97            a = newArr;
98 }

99 //This function will increase the key value of the node i in the heap by the amount specified by amount
100 void HeapIncreaseKey(Tuple a[], int i, int amount){
101            a[i] Value = a[i] Value + amount;
102            BuildMaxHeap(a);
103 }

CSE Helper